How Much Does a Student Loan Cost?

The cost of a student loan depends on more than just the interest rate. The real cost of a student loan depends on the cash flow characteristics of the student loan. The cash flow characteristics include how much money is received by the borrower and how much the borrower pays and how quickly.

Use our Student Loan Calculator to determine the monthly loan payment and total payments on your student loans.

The cash flow characteristics of a student loan are influenced by the terms and conditions of the student loan. The terms and conditions of the student loan determine how much money is received by the borrower to pay for college and how much the borrower pays back over time.

The Annual Percentage Rate (APR) is a popular metric for comparing the cost of different loans, but it is not effective at comparing the cost of loans with different repayment terms. A better approach is to use the repayment ratio, which compares the total payments to the net amount received.

Loan Characteristics that Affect the Amount Received

Loan fees, such as origination, default and guarantee fees, can affect the amount received by the borrower.

Borrowers can choose one of two different ways of dealing with the loan fees.

• Loan fees can be deducted from the disbursements, reducing the amount received by the borrower.
• Loan fees can be added to the loan balance, so that the borrower receives the specific amount of funding that the borrower is seeking after the fees are deducted. This increases the amount borrowed and thus the amount that the borrower will repay.

Student loan borrowers typically have the loan fees, if any, added to the loan balance.

Suppose that the borrower is borrowing a student loan with a loan balance of B and fees of F.

• If loan fees are deducted from the disbursement, the borrower will receive B – F x B. For example, if the borrower borrows a $10,000 student loan with 4% fees, the net disbursement will be $10,000 – $400 = $9,600.
• If loan fees are added to the loan amount, the new amount borrowed will be B / (1 – F). For example, if the borrower needs $10,000 from student loan with 4% fees to pay college bills, they will need to borrow $10,000 / (1 – 4%) = $10,416.67. Subtracting 4% in fees from $10,416.67 yields a net disbursement of $10,000.

Whether the fees are deducted from the disbursement or added to the loan balance, the fees have the same impact on the loan costs per dollar received or per dollar borrowed, as the costs are proportional.

Loan fees are a form of up-front interest. Each 4% in fees is about the equivalent of a 1% increase in the interest rate on a 10-year repayment term and a 0.5% increase in the interest rate on a 20-year repayment term.

Loan Characteristics that Affect the Amount Repaid

There are several loan characteristics that affect the amount the borrower will repay.

• Interest Rate
• Subsidized Interest Benefits
• Capitalization of Interest (Compounding)
• Interest Capitalization Frequency
• Borrower “Touch” Payments During the In-School and Grace Periods (Full Deferment vs. Fixed Payments, Interest-Only Payments and Principal and Interest Payments)
• Duration of Deferment, Grace and Forbearance Periods
• Type of Repayment Plan
• Length of the Repayment Term
• Loan Forgiveness Options

Generally, a smaller monthly payment increases the repayment term and the total interest paid. About two-thirds of borrowers are in a 20-year or longer repayment plan.

Periods during which there is no loan payment increase the cost of the loan unless someone else is paying the interest on the loan. Examples include the in-school and grace periods, the economic hardship deferment, the unemployment deferment and forbearances.

Annual Percentage Rate (APR)

The Annual Percentage Rate (APR) attempts to provide a standardized basis for comparing the cost of different loans. But, there are several flaws with the APR that affect the usefulness of the APR for evaluating the cost of a loan.

The Annual Percentage Rate (APR) combines the impact of a loan’s interest rate and fees on the cost of the loan, expressed as an annualized percentage rate.

The APR rolls up the loan fees and nominal interest rate into a single equivalent interest rate. The APR will usually be higher than the loan’s nominal interest rate.

The formula for the APR is

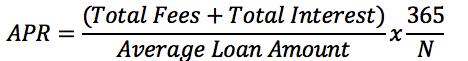
where N is the number of days in the loan term.

The APR does not consider the impact of compounding, just simple interest. This is in contrast with the Annual Percentage Yield (APY), which considers the impact of compounding. The APY is also known as the effective annual rate (EAR).

If the interest rate is 4.529% and the fees are 1.059%, with a 10-year repayment term, the APR is 4.76%.

The formula for the APY is 

where N is the number of compounding periods per year. For example, the Daily Periodic Rate is APR/365.

The interest capitalization frequency may vary by loan. For example, credit cards have interest compounded on a daily basis, while student loans may have interest compounded on a daily, monthly, quarterly or annual basis, or just at loan status changes.

If APR is 5%, then APY is 5.116% compounded monthly and 5.127% compounded daily.

Flaws in the APR

The Truth in Lending Act (TILA) requires consumer loans, such as private student loans, to list the APR in addition to the nominal interest rate.

But, the APR is particularly ineffective when comparing loans with different repayment terms or different repayment plans, as often occurs with student loans.

For example, consider two loans with different repayment terms but the same interest rates and fees. The loan with the longer repayment term will have a lower APR because the fees are spread out over a longer repayment term. But, a longer repayment term yields an increase in the total payments over the life of the loan and an increase in the total cost of the loan.

A longer repayment term can even be used to mask higher fees. For example, consider two loans with a 5% interest rate. One has 4% in fees and a 10-year term and the other has 7.1% in fees and a 20-year term. Both have an APR of 5.89%.

The monthly payment may be lower on the loan with the longer repayment term, $7.10 vs. $11.05 per $1,000 borrowed, but the total amount paid will be much higher, $1,705 vs. $1,326 per $1,000 borrowed.

The APR also does not reflect the total cost of borrowing because some fees aren’t included in the calculation of the APR. For example, late fees and collection charges are ignored. Deferments and forbearances are also ignored. Even if the APR considers the impact of the in-school and grace periods, there is no standardization of the weighted average length of the in-school period. The APR also doesn’t consider whether the borrower will pay off the loan early.

Ratio of Total Payments to Net Disbursements

An alternative is to consider the ratio of total payments to net disbursements on the loan. Call it the repayment ratio. The repayment ratio measures the cost of the loan as a percentage of the amount originally received.

Unlike the APR, the repayment ratio does not bias the results in favor of a longer repayment term, since the result is not annualized.

For example, here are repayment ratios for federal student and parent loans, based on the interest rates and loan fees for 2019-2020:

The in-school and grace periods typically increase the repayment ratio on unsubsidized loans by a factor of 1.1 to 1.25.

A more sophisticated analysis would use a discount rate to calculate the net present value of the repayment ratio, so that payments made later in the repayment term are worth less than payments made earlier.

Sign up for our free student loan newsletter for more expert advice on how to avoid student loans, borrow responsibly and manage repayment.